本篇文章观点仅限于目前的理解，后续若有新的理解，还会继续更新。
0. Introduce
Batch Normalization出现后基本取代了局部响应归一化操作(LRN)，目前已经成为CNN网络的标准配置。 BN操作通常用于卷积层和激活层之间，用于对各层的feature map进行归一化操作。 目前对BN操作的理解仍然有限，本篇文章首先分析CNN网络中对数据进行归一化的目的，然后分析BN的算法流程，最后分析BN操作对CNN网络带来的影响。
1. Normalization
机器学习中经常会提到正则化(Regularization)/归一化(Normalization)和标准化(Standardization)，其中正则化是一种通过在Loss函数后添加正则项来防止过拟合的方法，根据在正则项中对目标变量求1-norm或2-norm可将正则化分为L1-norm和L2-norm，而归一化和标准化则是指对数据的不同处理方式，这其中的一些概念容易混淆。
事实上归一化和标准化都是属于四种特征缩放(Feature Scaling)方法，分别如下：
- Rescaling(min-max normalization)，有时简称normalization:$x^{‘}=\frac{x-min(x)}{max(x)-min(x)}$
- Mean normalization:$x^{‘}=\frac{x-mean(x)}{max(x)-min(x)}$
- Standardization(Z-score normalization):$x^{‘}=\frac{x-mean(x)}{\sigma}$
-
Scaling to unit length:$x^{‘}=\frac{x}{ x }$
上述四种特征缩放方法，前两种(尤其是第一种)常被称作归一化(Normalization)，第三种常被称作标准化(Standardization)，在论文中有时也很少出现标准化(Standardization)，而是将上述前三种同一称为归一化(Normalization)方法。
第一种归一化方法将数据缩放到[0, 1]，第二种则将数据缩放到[-1, 1]且均值为0。第一种方法在有外点出现时则性能则性能不好。
第三种归一化方法应用最为广泛，通常对特征进行预处理，将其缩放到均值为0， 方差为1的空间。
可以简单理解为，前两种归一化方法主要的目的就是把数据映射到[0, 1]或[-1, 1]，可消除量纲，同时便于后续的数据处理，而第三种归一化方法则是将数据按比例缩放到一个特定小区间，如下图所示：
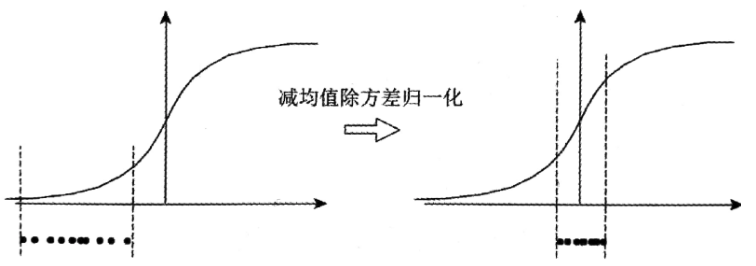
通过上面的内容，应该大致可以分清归一化和标准化，Batch Normalization中的Normalization对应着上述的第三种归一化操作。
2. Batch Normalization
机器学习领域对数据都由一个i.i.d 独立同分布假设，也即是假设训练数据和测试数据满足相同的分布，因此在训练数据上获得的模型可以在测试数据上获得比较好的结果。
因此，通常预先对数据进行白化(whitening)处理，以去除特征之间的相关性并使特征满足相同的分布。在有关图像处理的一些实验中发现，如果预先对输入图像进行白化，也即将其变换到均值为0，方差为1的正态分布上，则网络会较快收敛。
基于上述发现，BN的作者推论，根据CNN网络的结构，每一层都是下一层的输入，若对每一层的结果都进行白化处理，则效果会不会更好？BN基本上就是遵循这种思想。
在论文中，作者提出了Internal Covariate Shift问题，简单来说就是在网络学习的过程中，参数在不断变化，这会导致各个隐层的feature map的分布也在不断变化，所以BN就是来强制将各个层的数据的分布变换到均值为0，方差为1的正态分布上。
下图是BN的流程图，该流程图是一个通用的流程图，其中m表示batch大小，x表示某一维的特征，下标表示该特征在不同batch的值，在当前batch中对该维特征求均值和方差（除的是标准差），然后进行归一化：
上图中的第四步是BN中比较关键的一步，经过归一化后的数据$x$基本会被限制在正态分布中心附近的范围内，作者表示这使得网络的表达能力下降，为了解决该问题，作者引入了两个参数$\gamma$和$\beta$，这两个参数在网络训练时通过学习得到，通过该线性映射可将正态分布进行左右移动或改变胖瘦，避免表达能力下降的问题。
下图是一个较完整的流程图，1-8步表示在网络训练中同时使用BN，9-12步表示在推理阶段使用BN，从第10步可以看出，推理阶段使用的均值方差等参数是训练阶段各个mini-batch的参数的均值：
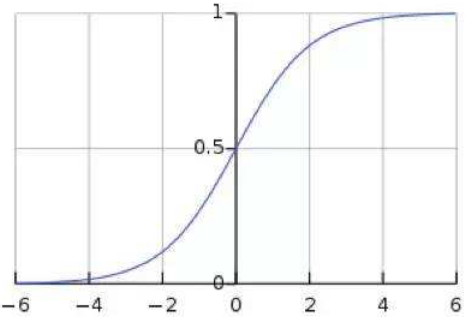
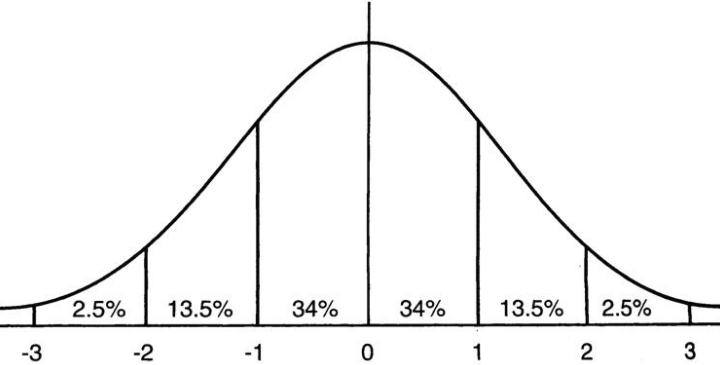
从激活函数的角度来考虑BN操作带来的影响，下图是Sigmoid函数的图像和正态分布的图像，若网络中每一层都使用BN进行处理，则每一层将有95%的数据落入[-2, 2]的区间，这在很大程度上可避免梯度消失的问题，并可加速训练：
3. Affect to CNN
以上的描述仅是BN的一种通用思想，若按照上述描述，则对CNN网络，需要分别对每个feature map的每个特征点分别计算均值方差并学习$\gamma$和$\beta$参数。 作者在论文中指出，为了遵循卷积网络的性质(此处应该指参数共享的性质)，所以在卷积网络中，BN操作是以feature map为单位的，每一层的feature map是由一个卷积核卷积得到的，则在进行BN操作时，把每层feature map作为一个单位(相当于把一个feature map视为某一维特征x)，在训练时，把每个mini-batch的相应层的feature map放在一起求均值和方差，对每个feature map学习一对$\gamma$和$\beta$参数。
设上一层卷积层的输出为x，激活函数为g，则原来的计算相当于y=g(Wx+b)，而有了BN后，则相当于y=g(k(Wx+b)+b')，因为BN中的线性变换存在偏置项b'，且求均值和方差的操作使得卷积时的偏置项b没有太大意义，所以在包含BN的卷积层中，一般省略b，则变换简化为y=g(kWx+b')。
BN对CNN的一些提升如下：
- 大大加快训练时的收敛速度；
- 论文中作者表示BN还有类似Dropout的正则化效果，所以使用BN后基本可不用使用Dropout；
- 对初始权重要求变低，且可使用较大权重;
